Topology

1Integrate allows data loaded within a session to be topologically structured. Topology structuring consists of snapping together feature geometries of different classes.

Topology structuring uses a tolerance value (see Tolerance) that is used to perform snapping on features in order to generate the relevant topology primitives such as nodes, edges and faces (see Topology Primitives).

Topology structuring provides a number of benefits:

• Data cleaning by snapping feature geometries together, such as to fix gaps, overlaps, undershoots and overshoots
• Accurate and unambiguous inter-geometry analysis, such as finding the length of shared boundaries between polygons
• Efficient analysis of inter-geometry problems, such as holes or overlaps in a polygon coverage

• Powerful data enhancement, such as forming polygons from the areas enclosed by a set of lines, or splitting lines where they cross Example.

  You may want to create polygons on your line data by using the geometries of the faces formed. In this example, we are building topology on the ROAD class and creating polygons from the face geometries.

  Within this action we have a Condition check to test whether or not the face we have is the universe face. If it is not the universe face, we will use it to build a polygon object of the class STREET_POLYGONS.

  

• Powerful data modification while retaining data connectivity, for example, simplifying polygon boundaries while keeping polygons connected

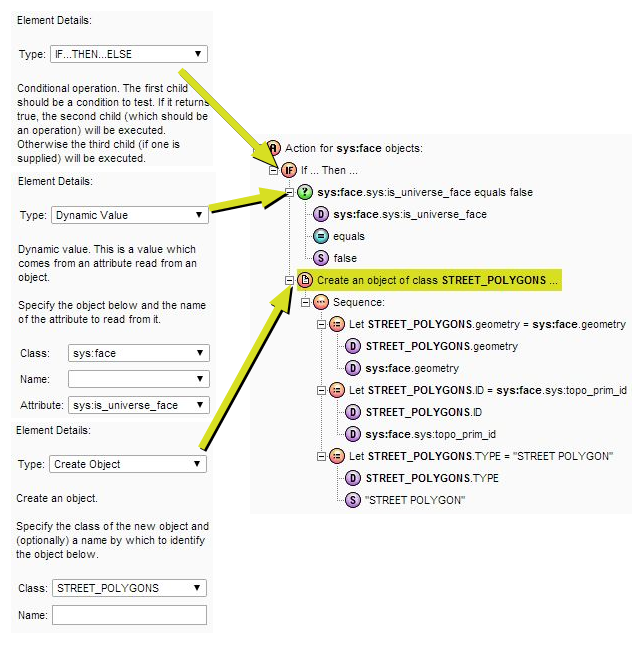
Once created, rules or actions can operate on the topological nodes, edges or faces as well as on the source feature objects that were used to build the topology. The references that connect the topology and the source features can be accessed within the rule logic.

Topology is performed via topology tasks (see Build Topology Task).