Relationships
A relationship compares any two values and returns a result of true or false.
They can either compare scalar values or spatial geometries.
Scalar Relationships
A scalar relationship compares any two values (boolean, integers, real numbers, dates or strings).
The result is evaluated as true or false, returning true if the values have the specified relationship.
Relationships include equal, not equal, less than, greater than etc., as well as relationships specifically for string: contains, begins with, ends with or matches a regular expression.
| Scalar Relationship | Description |
|---|---|
| Equal |
The two values are the same. |
| Not Equal |
The two values are different. |
| Less Than |
The first value is less than the second value. |
| Less Than or Equal |
The first value is less than the second value, or the two values are the same. |
| Greater Than |
The first value is greater than the second value. |
| Greater Than or Equal |
The first value is greater than the second value, or the two values are the same. |
| Begins With |
For string values, test whether the first string begins with the second string. |
| Ends With | For string values, test whether the first string ends with the second string. |
| Contains | For string values, test whether the first string contains the second string. |
| Regular Expression | For string values, check whether the first string matches the wild card string or Perl regular expression in the second string. |
Spatial Relationships
A spatial relationship is a type of relationship only applied to geometry values. It returns true if the geometries have the specified relationship.
Any type of geometry can be passed into a spatial relationship check, but only the geometry types relevant to this spatial relationship will be tested. For example, if comparing areas, line geometries will not be tested.
Note: Some spatial relationships can be considered subsets of others. For example, Covered By is a subset of Within (if a geometry is Covered By another geometry, it is also Within that geometry).
The detailed description of each spatial relationship uses the terms interior, boundary, exterior. See Geometries for more information on these terms.
![]() Types of Spatial Relationships
Types of Spatial Relationships
| Spatial Relationship | Description |
|---|---|
| Beyond |
Beyond checks that the geometry is at least a certain distance away from another (specified in dataset units). The order of the geometries does not matter. Note: Beyond is the opposite of Within Distance. |
| Contains |
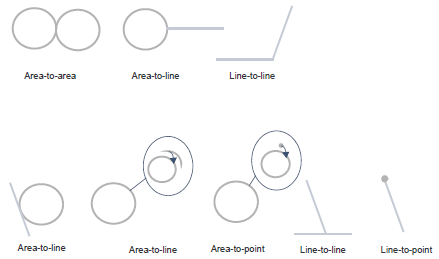
Contain means that the other geometry is completely inside this line or polygon (one object's boundary and interior are inside another). Note: Their boundaries are allowed to intersect, so it includes the Cover and Equal relationships. For lines the boundary means the end points, and for polygons the boundary means all inner and outer rings. The types of geometries that can contain another are:
Contains geometries Note: Contains is the reciprocal of Within. |
| Covered By |
Covered By is a special case of Within. It is only true when this geometry is contained within another, and their boundaries intersect (so they share some boundary). For lines the boundary means the end points, and for polygons the boundary means all inner and outer boundary rings. The types of geometries which can be covered by another are:
Note: Covered by is the reciprocal of Covers. |
| Covers |
Covers is a special case of Contains. It is only true when the other geometry is contained within this one, and their boundaries intersect (so they share some boundary). For lines the boundary means the end points, and for polygons the boundary means all inner and outer boundary rings. The types of geometries which can cover another are:
Note: Covers is the reciprocal of Covered By. |
| Cross |
Two geometries Cross when a line runs across the boundary of an area, or the interior of another line. Note: At least one of the geometries must be a line. The types of geometries which can cross are:
The order of the geometries does not matter.
Cross geometries |
| Disjoint |
Disjoint means that the geometries do not intersect at all (neither the boundaries nor the interiors intersect). The order of the geometries does not matter. Note: Disjoint is the opposite of Intersect. |
| Equal |
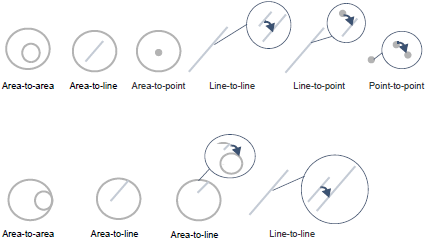
Two geometries are Equal when they are identical (they have the same interior, boundary and exterior). Geometries do not need to have the same number of vertices (as long as they follow the same path, within geometric tolerance), and lines do not need to have the same direction. Polygon boundaries do not have to use the same start/end vertex in order to be equal. The order of the geometries does not matter. The types of geometries which can be equal are:
Equal geometries |
| Intersect |
Intersect means any sort of spatial interaction. It checks that either the boundaries or interiors of two geometries intersect in any way, using any of the following relationships:
The order of the geometries does not matter. Note: Intersect is the opposite of Disjoint. |
| Overlap |
Two geometries Overlap when two lines or two areas partly overlay each other. Overlap means geometries are partly inside and partly outside each other (so does not include being contained or being equal). The types of geometries that can overlap are:
The order of the geometries does not matter.
Overlap geometries |
| Touches |
Touch means that the boundaries intersect but the interiors do not. For lines the boundary means the end points, and for polygons the boundary means all inner and outer rings. Adjacent polygons or end-to-end lines touch. The types of geometries that can touch are:
The order of the geometries does not matter.
Touch geometries |
| Within |
Within means this geometry is completely inside the other, which must be a line or polygon. Their boundaries are allowed to intersect, so it includes the Covered by and Equal relationships. For lines the boundary means the end points, and for polygons the boundary means all inner and outer rings. The types of geometries which can be within another are:
Within geometries Note: Within is the reciprocal of Contains. |
| Within Distance |
Within Distance checks that the geometries approach within a specified minimum distance of each other (specified in dataset units). The order of the geometries does not matter. Note: Within Distance is the opposite of Beyond. |