Topology Types
The topology of a set of geometries can be represented as a linear network topology or as a planar topology.
Network Topology
A network topology uses node and edge primitives to describe interconnected linear features and points on a map or the boundaries of polygons.
- Edges can represent such features as roads, railways, power lines and rivers.
- Nodes are used to represent such features as junctions in a transport network, valves in a pipeline, or stops on a bus route.
Network topology is useful for detecting dead ends or unsplit lines. You can create network topology even if your data contains polygons. Structuring is faster in network topology and more accurate. However, some functions require planar topology.
The example below shows a simple road network and the corresponding topological representation consisting of nodes and edges. The roads are represented by the edges between the nodes. The towns, road intersections, and the bus stop are represented by nodes.
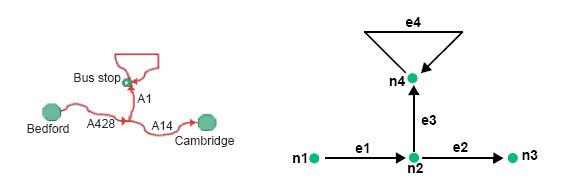
Example topological representation of a road network
Network topology makes it possible to create queries without having to compare geometries at every junction. The topological data enables the information to be obtained by a simple relationship query. The alternative, without the topology model, would be to infer the information from the feature geometry through the less efficient process of multiple direct spatial comparisons.
Planar Topology
Planar topology uses face primitives in addition to nodes and edges to describe two-dimensional areas on a map.
A face is formed within every closed set of edges.
The example below shows how areas in an imaginary land parcel can be described in terms of nodes, edges and faces. The land parcel consists of an area called Great Lingford, which contains three administrative areas (Norton, Weston and Easton). Each administrative area is represented by an individual face, while Great Lingford consists of three faces.
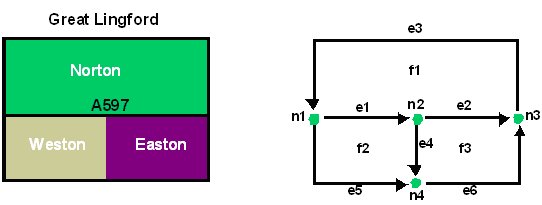
Example topological representation of areas within a land parcel
Describing area topology in terms of faces and boundaries makes it easy to determine the adjacency and containment properties of an area without analysing the geometry of the area.

